[Data Structure] Tree

20 Nov 2024 in Algorithm / Data Structure on Data-structure

• Introduce
• 용어 정리
• 특징
• 종류

Introduce

트리(Tree)는 자료구조에서 그래프(Graph)의 하위 개념 중 하나이며, 하나의 노드(Node)가 여러 간선(Edge)를 통해 자식 노드(Child Node)를 가리킬 수 있는 비선형적 자료구조이다.
그래프에서 트리를 별도로 분류한 이유는 트리는 일반적인 그래프와 달리, 계층 구조(Hierarchial structure)를 갖는 특수성 때문이다.
트리(Tree)는 순서보다 데이터 구조의 계층적인 상하관계를 표현할 때 주로 사용된다.

용어 정리

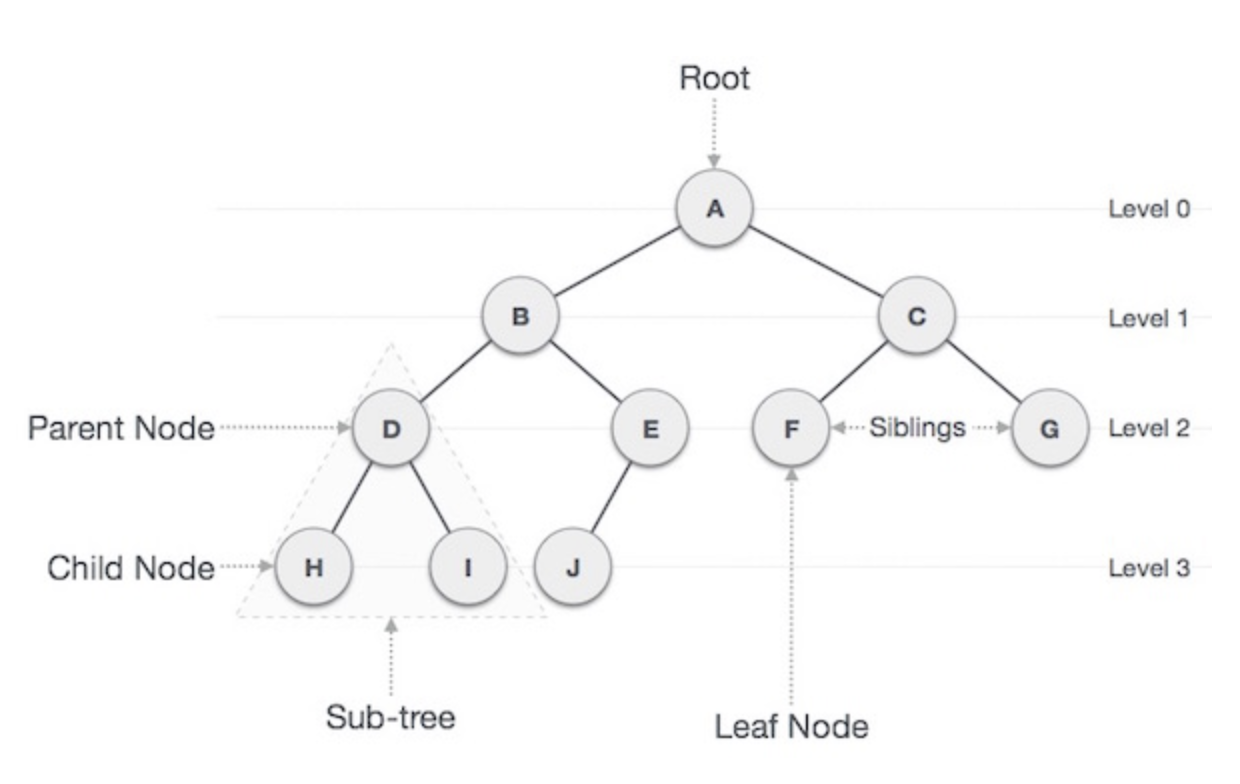
이름	정의	예시
노드(Node)	Tree를 구성하고 있는 기본 요소	A, B, C, D, E, F, G, H, I, J
간선(Edge)	Node와 Node 간의 연결선
루트 노드(Root Node)	Tree 구조에서 Parent Node를 갖지 않는 최상위 Node	A
부모 노드(Parend Node)	Child Node를 갖는 Node	H, I Node의 Parent Node: D
자식 노드(Child Node)	Parent Node의 하위 Node	Node D의 Child Node: H, I
형제 노드(Sibling Node)	같은 Parent Node를 갖는 Node	H, I는 Parent Node D를 갖는 Sibling Node
단말 노드(Terminal Node)	Parent Node가 없는 Node	H, I, J, F, G
깊이(Depth)	Root Node에서 특정 Node까지의 Edge 수	Root Node Depth: 0, Node D Depth: 2
높이(Height)	특정 Node에서 Termial Node까지 가장 긴 경로의 Edge 수	Node A Height: 3

특징

• 하나의 Root Node와 0개 이상의 하위 Tree로 구성
• 데이터를 순차적으로 저장하지 않으므로 비선형 자료구조
• Tree내에 또 다른 Tree가 있는 재귀적 자료구조
• 단순 순환(Loop)을 갖지 않고, 연결된 무방향 그래프 구조
• Node간에 부모 자식 관계를 갖으며, 계층형 자료구조(모든 Chile Node는 하나의 Parent Node만 갖는다.)
• Node가 N개인 Tree는 항상 N-1개의 Edge을 갖는다.

종류

• 편향 트리(Skew Tree)
  • 모든 Node들이 Child Node를 하나만 갖는 Tree
  • 왼쪽 방향으로 Child Node를 하나씩만 가질 때 Left skew tree
  • 오른쪽 방향으로 하나씩만 가질 때 Right skew tree
• 이진 트리(Binary Tree)
  • 노드의 간선이 최대 두개로만 구성된 트리
• 이진 탐색 트리(Binary Search Tree, BST)
  • Node의 왼쪽 자식은 부모의 값보다 작은 값을 가져야 하며, Node의 오늘쪽 자식은 부모의 값보다 큰 값을 가짐.
  • Node의 데이터 값은 중복을 허용하지 않는다.
  • Node의 데이터 값은 nil이 될 수 없다.
• m 원 탐색 트리(m-way search tree)
  • 최대 m개의 서브 트리를 갖는 탐색 트리
  • 이진 탐색 트리의 확장된 형태로 높이를 줄이기 위해 사용
• 균형 트리(Blanced Tree, B-Tree)
  • m원 탐색 트리에서 높이 균형을 유지하는 트리